动态规划算法

总方法论 - 动态规划五部曲

  1. 确定DP数组（DP table）以及下标的含义
    • 动态规划的核心在于理解和明确DP数组所表示的含义
    • 在进行动态规划递推公式推导的时候要紧紧围绕着DP数组的含义
  2. 推导递推公式
    • 推导递推公式的关键在于找到当前状态可以由哪些状态转移而来
    • 要搞清楚可以从哪些状态转移来就要紧紧围绕着DP数组的含义
  3. dp数组如何初始化
    • 在确定递推公式之后在进行初始化

  4. 确定遍历顺序

  5. 举例推导dp数组
    • 如果动规结果不正确，最好的方式是打印出来DP数组的值，分析与预期结果哪里不正确

动态规划：01背包理论基础

01背包问题基本题目（二维数组解法）：

题目描述
有个背包可承受重量N，现有T件物品，每件物品重量为Wi,价值为Vi ,每件物品只有一个,这个背包可以装载物品的最大价值是多少?
输入格式
第一行，两个整数，分别表示N和T，用空格隔开（N≤1000，T≤100）
接下来T行，每行两个整数，分别表示T件物品的重量Wi和价值Vi（1≤Wi,Vi≤100）
输出格式
一行，表示这个背包可以装载物品的最大价值
输入输出样例
输入样例1：
100 5
77 92
22 22
29 87
50 46
99 90
输出样例1：
133

模拟过程(画图)可以参考：背包理论基础01背包-1

分析

  1. 状态转移过程
    dp[i][j]的转移可以由它的上方（dp[i-1][j]）和左上方转移（dp[i-1][j-weights[i]] + values[i]）而来
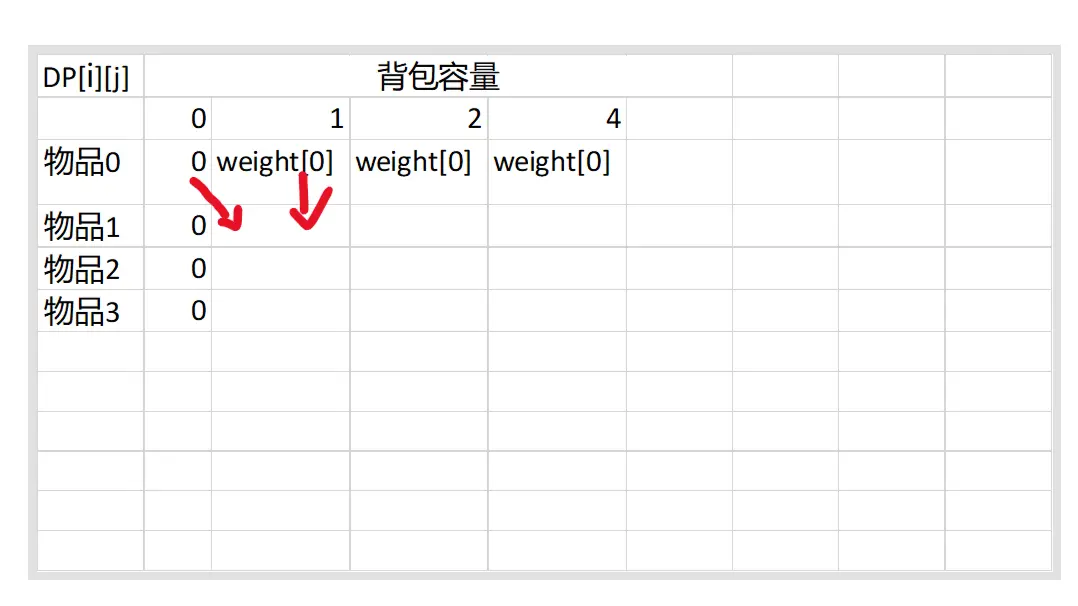
    算法-01背包-1

  2. dp[0][j] 和 dp[i][0] 的初始化

    • dp[i][0] 初始化为0，因为在背包载重为0时总价值肯定全为0
    • dp[0][j] 第一行表示装第一个物品后背包的价值（对应dp[0][i] = values[0]）
      如果背包的载重装不了第一个物品则价值还是为零（对应i = weights[0]，也就是从背包载重能满足第一个物品开始

  3. DP数组的其他值该如何初始化？

    • 都可以，0、-1、-100都没有关系，因为DP数组的其他值都是由之前的状态转移而来的

  4. 遍历顺序，填充DP数组

    • 那么问题来了，先遍历 物品还是先遍历背包重量呢？
    • 其实都可以！！ 但是先遍历物品更好理解。
      • 物品的遍历从第二个开始
      • 背包重量的遍历从0开始
      • 如果背包重量小于当前物品的重量，那么就继承dp[i - 1][j]的值
        if(j < weights[i]) dp[i][j] = dp[i-1][j];

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
using namespace std;

int n,t;
/*
dp[i][j] 的含义是表示从下标为[0-i]的物品里任意取放进容量为j的背包
，价值总和最大是多少
*/
int dp[100+10][1000+10];
int weights[100+10];
int values[100+10];
int main() {
    cin>>n>>t;
    for(int i = 0;i < t;i++){
        cin>>weights[i]>>values[i];
    }
    
    //初始化DP数组
    /*
    1. 背包承重为0，第一列全初始化为0（对应的dp[][0] = 0）
    2. 第一行表示装第一个物品后背包的价值（对应dp[0][i] = values[0]）
        如果背包的载重装不了第一个物品则价值还是为零（对应i = weights[0]，
        也就是从背包载重能满足第一个物品开始
    */
    for(int j = weights[0]; j <= n; j++){
        dp[0][j] = values[0];
    }
    
// 递推公式：dp[i][j] = max(dp[i-1][j],dp[i-1][j-weights[i]] + values[i]);
/*
dp[i][j] 可以由两个状态得到：
1. 放物品i  ----> dp[i-1][j]
2.不放物品i ----> dp[i-1][j-weights[i]] + values[i]

在两者中取其大
*/
    
    // 先遍历物品再遍历背包容量
    for(int i = 1; i < t; i++){   // 遍历物品(从第二个物品开始遍历)
        for(int j = 0; j <= n; j++){  // 遍历背包容量
            // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
            if(j < weights[i])  dp[i][j] = dp[i-1][j];
            else{
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-weights[i]] + values[i]);
            }
        }
    }
    
    cout << dp[t-1][n];
    return 0;
}

01背包问题（一维数组解法）

注意点：

  1. 为什么可以不对第一行进行初始化
    因为在后续的滚动过程中就相当于完成了这个初始化过程
  2. dp[i] 的含义容量为i的背包，所背的物品价值可以最大为dp[i]
  3. 为什么在使用滚动数组的时要倒序遍历背包容量
    因为如果使用正序遍历，在计算dp[i]时会用到dp[i-1]，而这时dp[i-1]已经被修改了，
    倒序遍历是为了保证物品i只被放入一次，如果一旦正序遍历了，那么物品0就会被重复加入多次！
  4. 使用滚动数组二重循环能否调换顺序
    不可以！
    因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
    题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;

int n,t;
/*
dp[i] 的含义容量为i的背包，所背的物品价值可以最大为dp[i]
*/
int dp[1000+10];
int weights[100+10];
int values[100+10];
int main() {
    cin>>n>>t;
    for(int i = 0;i < t;i++){
        cin>>weights[i]>>values[i];
    }
    
    //使用一维数组时可以不对第一行进行特殊的初始化
    //因为在后续的滚动过程中就相当于完成了这个初始化过程

    // for(int j = weights[0]; j <= n; j++){
    //     dp[j] = values[0];
    // }
        
    // 先遍历物品再遍历背包容量
    for(int i = 0; i < t; i++){   // 遍历物品(从第1个物品开始遍历)
        for(int j = n; j >= weights[i]; j--){  // 倒序遍历背包容量
            dp[j] = max(dp[j],dp[j-weights[i]] + values[i]);
        }
    }
    
    cout << dp[n];
    return 0;
}